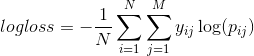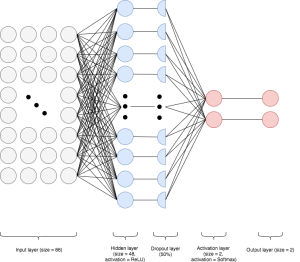Hockey, perhaps more than any other major sport, is difficult to predict. In the NHL, enforced parity and the intrinsic randomness of the game conspire to shorten the gap that exists between the league’s best and worst clubs. Michael Lopez concludes that the better NHL team can expect to win 57% of matches played against an opponent on neutral ice. That number places the league only slightly above the MLB (56%) and well behind the NBA (67%) and NFL (64%).
This video, albeit much less exhaustive than Lopez’s research in methodology, does a good job of summarizing the agents of randomness and their impacts on various sports:
Again, we find that hockey is comparatively prone to variance.
If you’re still not convinced, Josh Weissbock claimed a theoretical upper bound exists for NHL game prediction accuracy of 62% in his 2014 thesis. That means even the best predictive models should expect to be wrong on 4 of 10 picks, on average.
Surprise, surprise. Hockey games are difficult to predict.
You’ll note that “difficult” does not mean “impossible,” nor does it make the endeavour less worthwhile. This distinction begs to be made in defence of the merit of analytics in hockey, which remains under siege by skeptics who believe the sport is somehow above being measured.
Weissbock caps one’s ability to correctly predict winners at 62%, and we can define a simple baseline of 50% given by the accuracy of a purely random algorithm (a coin flip). Better yet, we can validate an extremely naive model: one that chooses the home team regardless of perceived team quality or circumstantial considerations. Such a model would score an accuracy of 54.7% spanning all regular season and playoff games between the 2007-2008 and 2016-2017 seasons. This serves as a useful benchmark against which we can measure predictive models. It is, in effect, the problem’s No Information Rate: the accuracy obtained from predicting the most common outcome (a home win) in each case. It stands to reason that any remotely successful statistical model should surpass this modest score.
However, prediction accuracy is insufficient to adequately measure a model’s performance. It is far less useful to simply predict an outcome from a set of possible classes than it is to produce a distribution of probabilities for said classes. In this instance, the probabilities assigned to a win for the home team and a win for the away team are of particular importance. Hence, a validation score that treats a misclassification of 55% and one of 95% equally is of limited use.
Log loss is an error function that penalizes overconfidence in incorrect predictions by introducing a logarithm term which tends to infinity as the probability of any class approaches zero.
The lower the Log Loss, the better a model is doing at predicting the likelihood of each possible outcome.
As with accuracy, we can establish Log Loss benchmarks by testing naive assumptions. Assigning equal probabilities to a home team win and an away team win (50/50) yields a Log Loss of 0.693 in the same sample of games as used afore. Applying the known rate of home wins found previously (54.7%) to this same set of games gives a score of 0.689. Again, these are ratings that one should expect to surpass with even a rudimentary approach.
In absence of a theoretical lower limit like that derived by Weissbock for prediction accuracy, we can at least mark the spot where a good model may fall. Let’s define good as a model that can contend against odds set by betting markets. Using the implied probability of a home win given by oddsmakers, Lopez find a Log Loss of 0.672. This value gives us something to strive for and some assurance that a model has value should it surpass this mark.
We have a ballpark, now it’s time to swing for the fences.
Over the Summer I developed a new prediction model. It is, by far, my most successful attempt to tackle this problem to date. I decided to call the model Salad.
Salad is an ensemble of 11 unique sub-models: 4 bagged logistic regression models, 1 XGBoost gradient-boosted trees model, 2 neural networks, 1 bagged naive Bayes model, 2 CatBoost gradient-boosted trees models and 1 random forest using fuzzy logic. Different feature sets were used among these sub-models in an effort to further increase diversity within the ensemble. A bagged logistic regression model was used for a stacking algorithm. My approach in building these ensemble components was loosely to optimize the mean score of the various models while minimizing collinearity. In plain terms, each of the sub-models should perform well on its own and no two sub-models should be overly alike in their output.
Before getting into each sub-model individually, I should outline my validation process. This testing suite will govern how well we measure our progress – this is both crucial and far too often overlooked.
Log Loss will serve as the loss function. Broadly, my objective in training and tuning a model is to minimize this score. However, since this is a prediction problem, we need to recreate the conditions of applying a prediction model to a new set of games.1This is called out-of-sample or out-of-bag. I used cross-validation to produce estimates of model performance on new data, and held out the entire 2016-2017 NHL season as a final testing set. Cross-validation was performed as follows: for each season contained in the training data, that season was held out once as a testing fold. Models were trained on all remaining training data except for the next season2The purpose of excluding the season that immediately follows the testing set from training is to prevent overlap between data sets. Among the features present in the training data were measures of team and player performance in the prior season. This exclusion policy prevents the possibility of models learning something about the testing data that they shouldn’t. , then scored according to their predictions on the held-out season. Scores were weighted by quantity of games present in the testing sample and averaged across all folds to give a validation score.
A feature matrix was constructed by combining various team statistics, measures of roster quality, and contextual elements. In total, the matrix contained 5,800 variables. The 2007-2008 season was removed due to the unavailability of necessary statistics from the prior season, and an imputation procedure was used to replace missing predictors in the remaining data. The imputation suite worked as follows:
For any cumulative in-season team statistic (for example, the home team’s 5-on-5 Goals For Percentage at the date of a given game in that same season), missing values (occurring whenever a team plays their first game of a season) were replaced with the equivalent statistic for that team in the prior season. Next, for any team statistic calculated over a time span in-season (for example, the home team’s 5-on-5 Goals For Percentage over the last 10 games played in that same season before a given game), missing values (occurring whenever a team has not yet played enough games to satisfy the time span) were replaced with the equivalent cumulative value of the statistic for that team. Lastly, for any metrics indicating the quality of a team’s staring goaltender (for example, the home starter’s Save Percentage at the date of a given game in that same season), missing values (occurring whenever data on that player is unavailable) were replaced by the mean value of that metric.
Further processing of the data was performed prior to model training. Each feature was normalized using centring and scaling, then any remaining missing values were assigned the median value of that particular feature.
This process, any data scientist will tell you, is by far the least enjoyable part of building a statistical model. It’s less enjoyable yet to read about it, so let’s move on.
Feature Sets
The 5,800 variables contained in the training data were divided into 7 feature sets. Some of these sets were manually defined, others were automatically generated from analysis of the data. In the instance of manually selected features, my selections were informed by a combination of past experience, variable importance calculations and validation results. Below is a summary of these feature sets:
Set #1: Broad team statistics (44 variables)
Set #2: Broad roster quality statistics (52 variables)
Set #3: Limited important3In this case, as determined by yours truly. features (16 variables)
Set #4: Principal Components (15 variables)
Set #5: Important4In this case, as determined by a random forest algorithm. 10,000 decision trees were grown using 200 randomly sampled observations and 100 features randomly sampled from the entire set. Variable importance is given by the mean decrease in out-of-bag accuracy between trees containing the variable and those not containing the variable. Variables with a mean decrease of 2% or more were kept. features (1,079 variables)
Set #6: Broad team and roster quality statistics (86 variables)
Set #7: All features (5,800 variables)
I opt not to reveal the exact contents of each feature set in order to preserve some intellectual ownership. Among the more important features, though, are:
- Cumulative team K
- Adjusted 5-on-5 Fenwick +/- per 60 in last 20 GP
- Mean WAR5The WAR metric used is my own yet-to-be-published version Quality of Roster
- Mean Star Rating6An improved version of the model explained here: https://corsica.hockey/blog/2017/02/27/probabilistic-forecasting-and-weighting-of-three-star-selections/ per game Quality of Roster
Sub-Model #1 – Logistic A
The first of 11 sub-models is a bootstrap aggregation of 100 regularized logistic regression models. Feature set #1 was used, and the lasso penalty was chosen for regularization. In each regression, a bootstrap sample was created from the training data by randomly sampling with replacement a number of observations equal to that of the total training set. A penalty term for each regression was determined by cross-validating a sequence of 100 values on 5 random folds within the bootstrap sample.
The regressions contained in the bag were each used to produce home team win probabilities for the testing folds, according to the validation suite detailed previously. These probabilities were averaged to yield a final model output. The cross-validation Log Loss score for this model was 0.6745.
Sub-Model #2 – Logistic B
The second of 4 bagged logistic regression models employs the same method as Logistic A. This model uses the feature set #2, however. The cross-validation score obtained for this model was 0.6753.
Sub-Model #3 – Logistic C
The same as Sub-Models #2 and #3, but with feature set #3. The cross-validation score obtained for this model was 0.6722.
Sub-Model #4 – Logistic PCA
Unlike the previous approaches, here, a new feature set is derived from the training variables using Principal Component Analysis. This procedure allows us to transform the entire variable set into a smaller collection of linearly uncorrelated components. Through trial, I found 15 Principal Components to be the most successful quantity. These comprise feature set #4. The cross-validation score obtained for this model was 0.6748.
Sub-Model #5 – XGBoost
This sub-model makes use of the XGBoost library for gradient-boosted decision trees. Feature set #5 was used in this case, and from each training fold, a 10% fragment of data was held out as an inner evaluation set. In each of 500 maximum iterations, 24 trees were grown in parallel on 5% of the training data and half of the total feature set. A maximum depth of 6 was enforced on all trees. Between iterations, a step is taken in direction of the gradient towards optimal tree structures. A relatively low learning rate was used. Early stopping was allowed to occur if the cumulative evaluation Log Loss did not improve in 30 epochs, in which case the best iteration was kept. The cross-validation score obtained for this model was 0.6742.
Sub-Model #6 – Neural Network A
A neural network classifier was built in TensorFlow using feature set #6. The network is comprised of an input layer of size equal to the number of input features (86), a hidden layer containing 48 neurons with ReLU activation, a 50% dropout layer, an output layer of size equal to the number of output classes (2), and finally, a softmax activation layer to yield interpretable probabilities.
As with XGBoost, an evaluation set was used to signal early stopping. In this case, however, the evaluation data was randomly re-sampled at every training iteration. The model was given 2,000 epochs and a low learning rate, with batch training in each epoch (50 observations per batch). Both learning rate decay and momentum were utilized for more efficient convergence. 50 epochs was used as a threshold for early stopping. The cross-validation score obtained for this model was 0.6760.
Sub-Model #7 – Neural Network B
The second neural network sub-model uses the same general framework as Sub-Model #6, but with feature set #3 serving as input. Further tuning of the hyperparameters was done to accommodate this new input shape. Namely, the number of hidden neurons was reduced to 12. The cross-validation score obtained for this model was 0.6737.
Sub-Model #8 – Naive Bayes
A naive Bayes algorithm was used with bagging to produce averaged probabilities. Feature set #6 was used, and 1,000 models were trained during each fold, each on a random sample representing 5% of the training fold and 8 variables selected from the total set. The mean output of these models serves as a final output. The cross-validation score obtained for this model was 0.6739.
Sub-Model #9 – CatBoost A
The CatBoost library offers a gradient-boosted trees algorithm similar to XGBoost. It was employed in addition to XGBoost in order to further diversify the methods within the eventual model ensemble. The CatBoost models also made use of different feature sets than the XGBoost model.
In this case, all available features (set #7) were used. The algorithm was given 20,000 iterations, training batches of size 50 and a very low learning rate, as well as a maximum tree depth of 4. Despite being provided no indication of feature importance, the CatBoost model produced a cross-validation score of 0.6744 – only narrowly worse than the XGBoost result.
Sub-Model #10 – CatBoost B
In contrast with Sub-Model #9, this CatBoost model used a very small feature set (#3). The parameters in this case were the same as described above. The cross-validation score obtained for this model was 0.6734.
Sub-Model #11 – Fuzzy Forest
The final sub-model I developed is by far the most experimental, and yielded the worst validation score. I opted to include it in the ensemble for the sake of diversity.
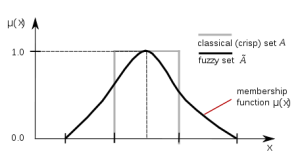
The basis of this approach is to transform our feature set into degrees of membership of linguistic classes using fuzzy logic. A fuzzifier will accept our normalized input matrix and return a new matrix containing values between 0 and 1 for each variable, for each of n desired classes. These values represent the degree to which an observation of this variable belongs to each of the n classes.
I opted for 5 classes, and employed the Gaussian membership function to derive degrees of membership:
Using the feature set #6 as the origin, the fuzzified data contains 430 (5 x 86) variables. One way to think of this abstracted data is in linguistic terms. Imagine that each observation of a variable in our set can be described as “very good,” “good,” “okay,” “bad” and “very bad.” Using fuzzy logic, we may find that a 53.4% 5-on-5 Goals For percentage has a 0.82 membership to “very good,” a 0.13 membership to “good,” a 0.046 membership to “okay” and negligible membership to either remaining class. This approach allows for a fresh perspective on a data set we’ve nearly already exhausted.
Rather than using a fuzzy-rule based classifier, I passed the fuzzified data to a random forest algorithm. 25,000 trees were grown, using 50 observations and 48 variables at random each time. The cross-validation score obtained for this model was 0.6773.
Ensembles
To fairly measure the result of a model ensemble, I first produced out-of-sample predictions from each sub-model using the same cross-validation procedure described afore. These predictions would serve as a “first layer” on which to train and test stacking algorithms.
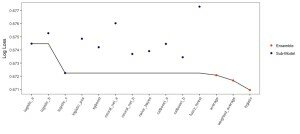
The first attempt made at combining sub-models was a simple average of each output. This method immediately superseded the most successful sub-model with a Log Loss of 0.6721. Although a promising start, this method makes a crucial oversimplification by omitting the relative quality of each constituent.
A logical successor to a sub-model average is a weighted average. In 100 random folds of the first layer, 90% of the data was used to compute the Log Loss of each sub-model’s out-of-bag predictions. These scores were then used to weight the predictions on the remaining 10%. An ensemble score was produced by averaging the Log Loss obtained from the weighted average on each of the 100 folds. This score again took first place, at 0.6717.
The final ensemble method was a bagged logistic regression resembling sub-models #1 through #4. 10 Regressions were produced on bootstrap samples of the out-of-bag probabilities (each equal in size to the original training data). This ensemble model was validated using the same procedure as for the weighted average. The score obtained was a Log Loss of 0.6709.
This is Salad.
This latest attempt at building a prediction engine for hockey represents a significant increase in complexity from what I’ve attempted in the past. However, I think the results obtained here justify it. In backtesting, Salad performs better than implied odds from Vegas in both Log Loss and accuracy.
Hockey is inherently random, but it isn’t roulette. With the right data and a little handiwork (a good computer doesn’t hurt either) though, you can make a decent go of it and even challenge Las Vegas.
References
| 1. | ↑ | This is called out-of-sample or out-of-bag. |
| 2. | ↑ | The purpose of excluding the season that immediately follows the testing set from training is to prevent overlap between data sets. Among the features present in the training data were measures of team and player performance in the prior season. This exclusion policy prevents the possibility of models learning something about the testing data that they shouldn’t. |
| 3. | ↑ | In this case, as determined by yours truly. |
| 4. | ↑ | In this case, as determined by a random forest algorithm. 10,000 decision trees were grown using 200 randomly sampled observations and 100 features randomly sampled from the entire set. Variable importance is given by the mean decrease in out-of-bag accuracy between trees containing the variable and those not containing the variable. Variables with a mean decrease of 2% or more were kept. |
| 5. | ↑ | The WAR metric used is my own yet-to-be-published version |
| 6. | ↑ | An improved version of the model explained here: https://corsica.hockey/blog/2017/02/27/probabilistic-forecasting-and-weighting-of-three-star-selections/ |