EP: This is a less technical adaptation of the original Hockey and Euclid guest post on WAR On Ice. The underlying math will be discussed briefly in the footnotes.
Spatial reasoning is an innate characteristic in humans. It allows us to intuit conclusions from imagery, which may be exploited by graphical representation of data.1For my money, Micah McCurdy belongs in a class of his own when it comes to hockey-related data viz. You can donate to his cause on Patreon. You’ve no doubt inadvertently benefited from this fact if you’ve ever gleaned information from a chart or visualization. Elements like proximity between points are more easily interpreted in this fashion than they are through the examination of numeric data. In many ways, this idea was the first building block of what would become a generalized method of computing statistical similarity between hockey players.
In two (and to a slightly lesser extent, three) dimensions, understanding and solving for proximity between points is a simple exercise. For all intents and purposes, the similarity that interests us is simply the inverse of the distance – something we’re taught how to calculate in basic trigonometry.2Pythagorean theorem Imagine plotting each NHL player-season by dimensions corresponding to their goal and assist rates. Neighbours clustering around a given point would represent that point’s (player’s) closest comparables in these two measures. Recall that similarity between data is inversely proportional to distance. Transitioning to Euclidean space allows us to generalize this approach for numbers of dimensions beyond the three we can visualize and interpret. We may now derive a standard similarity formula that functions in any number of dimensions.3Here, dimensions can be any numeric measure providing information about players.
One significant wrinkle in this approach is that we want to break free from the assumption that all dimensions are equally important. Thankfully, weights can easily be included in our formula. This allows for a great deal of flexibility. The distance equation4Where p0 and p1 are the origin and comparison points, respectively, i, …, n are the measures by which you are comparing and w are the corresponding weights. is as follows:
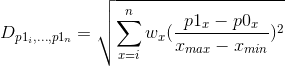
And the Similarity calculation:
![]()
The Similarity values may be interpreted as such: The Similarity between two players subtracted from 100 gives the percentage of the maximum allowable distance that is represented by the distance between the two positions occupied by the players. In other words, a 98% similarity between players would mean the distance between their positions in imaginary space is 2% of the largest possible distance that could exist between two points in the space bounded by observed values of each dimension. If you had plotted players according to G/60 and A/60 as described above, this maximum distance would be given by the distance between two corners of the plot.5Mathematically, this equates to each p1 – p0 term in the distance formula being equal to its denominator. The distance equation simplifies to the square root of the sum of all weights, thus the Similarity calculation gives 100 x (1 – 1) = 0.
By default, the Similarity Calculator returns only players of the same position. Because results are dependant on the selected weights, it’s important to be mindful of the conclusions you should or shouldn’t draw from them.
References
| 1. | ↑ | For my money, Micah McCurdy belongs in a class of his own when it comes to hockey-related data viz. You can donate to his cause on Patreon. |
| 2. | ↑ | Pythagorean theorem |
| 3. | ↑ | Here, dimensions can be any numeric measure providing information about players. |
| 4. | ↑ | Where p0 and p1 are the origin and comparison points, respectively, i, …, n are the measures by which you are comparing and w are the corresponding weights. |
| 5. | ↑ | Mathematically, this equates to each p1 – p0 term in the distance formula being equal to its denominator. The distance equation simplifies to the square root of the sum of all weights, thus the Similarity calculation gives 100 x (1 – 1) = 0. |

This similarity scores calculator is bookmark-worthy and a great reference tool for any fan of analytics.